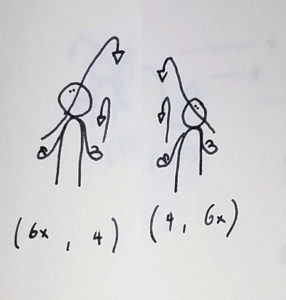Siteswap Fundamentals
Siteswap notation is a way that jugglers write patterns down. It was invented (or discovered – depending on who you’re talking to, that could be the start of a big, pedantic argument!) in the 1980s… by four people, at the same time, all independently of one another. (We’re not going to get into a discussion about emergent intelligence, but suffice to say this is an important tool that has shaped the face of modern juggling.)
Siteswap changed the way jugglers describe juggling patterns to one another – the conversation went from “throw a ball kinda high on one side to the same hand, then one with the other hand at the same height to the same hand, then pass one underneath those two while they’re in the air from one hand to the other, then throw that ball again like a normal juggling throw and keep doing a cascade after that” to “do 441333.” Useful, right?
When written, siteswaps look like a string of incoherent numbers to the untrained eye. 441, 97531, (6x,4)*… complicated stuff at first glance. So let’s look a little longer and break it down.
In music, written notes indicate how long a particular sound is played. You have full notes, quarter notes, eighths, and so on. In juggling, the number represents how long it takes for an object to return to a hand (or, perhaps more eloquently, the amount of time it takes for a ball to be re-thrown.) Lots of jugglers will use a shorthand, saying that the number means how long an object is in the air – that is, the height of the throw. Though that’s technically incorrect (more on that in a future post – for now, you’ll have to be satisfied with this workshop handout (700kb, .pdf,)) we’ll be using the idea of number-value and height interchangeably in this article.
When you juggle a three ball cascade, all of the throws are siteswap 3. That means that every thrown ball returns to a hand after three beats. A beat is an arbitrary measure of time – every juggler has their own internal metronome. Though it’s usually considered best to have tall, slow patterns, if you get two jugglers to juggle three balls side by side, their patterns will almost invariably have slightly different tempos. My 3 might be different than your 3.
…Part of this is due to throw height, but the other part is due to something called dwell time – the refractory period where the ball is resting in your hand. If you’re juggling three balls in a cascade with a long dwell time or if you’re juggling three balls in a cascade with a short dwell time, the throws are all still the same… Imagine a metronome that marks time with a short click and an metronome that marks time with a longer tone – it’s kind of like that. (If you’re interested in learning more about this, and the more-complicated-than-we-need-to-get-here aspects of juggling math, check out Shannon’s Theorem.)
All that said, the big takeaway for our purposes is that you’ve got an internal metronome that clicks out beats.
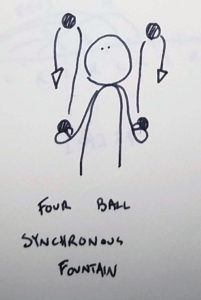
The three ball cascade is a relatively low pattern where everything crosses. As you probably know, the four ball fountain is a different pattern!
Why do we juggle odd numbers in a cascade and even numbers in a fountain? Well, let’s dive in!
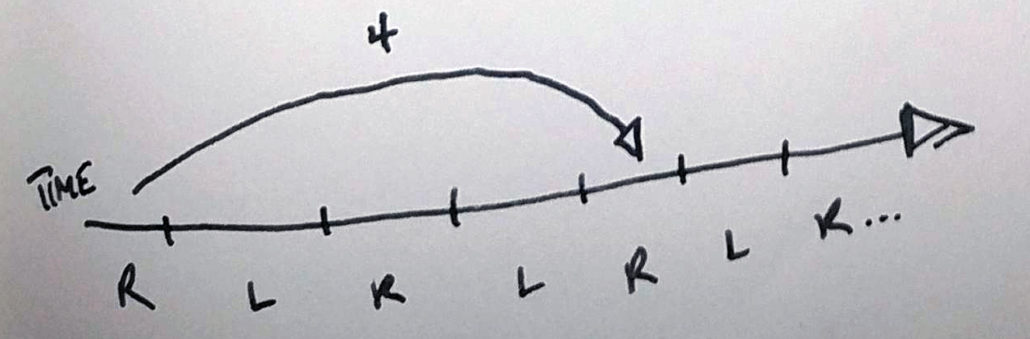
When you juggle a four ball fountain, all of the throws are siteswap 4. That means that every ball returns to a hand after four beats.
When you juggle a five ball cascade… (and I think you know where I’m going with this now…) all of the throws are siteswap 5. A six ball fountain? They’re all 6s. A seven ball cascade? They’re all 7s. And so on and so forth.
Looking at these diagrams, you might have noticed something. All of the odd-numbered throws cross the body – they’re thrown and caught by different hands. All of the even-numbered throws stay on the same side, and are thrown and caught by the same hand. Weird, right? Well, there’s a reason for it!
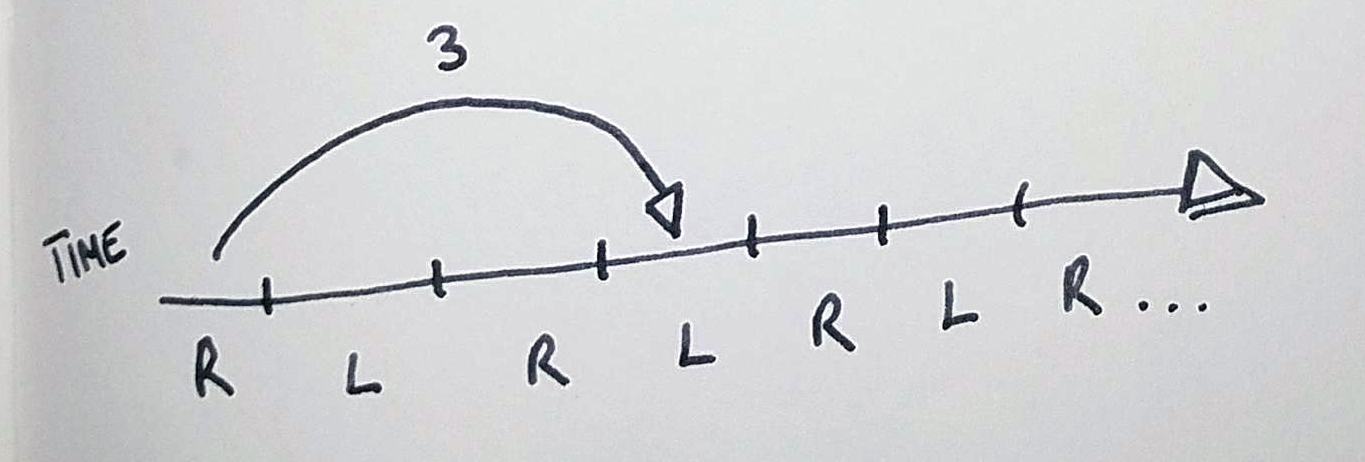
There are a few rules in siteswap, and the most important are that we must notate everything that happens on every beat (even if there’s nothing for that hand to do in that time!), and that your hands alternate beats. This means that when you look at a string of numbers, they’re alternating hands:
Right, left, right, left, right, left…
-Or, Left, right, left, right, left, right… if you’re left-handed. (Ha!)
So, if you’re throwing an object for an odd length of time – throwing a 3 or a 5 or a 7 – the object can’t be caught by the same hand that threw it.
If you’re throwing an object for an even length of time – throwing a 4 or a 6 or an 8 – the object must return to the same hand that threw it.
If this is all confusing, don’t worry! It took juggling scientists the better part of 4,000 years to arrive at this system – they figured this out so we didn’t have to. (Let’s hear it for someone else doing the work!)
The big takeaway here is this simple rule:
Odd throws switch sides. Even throws stay on the same side.
But Thom… what about the number 2? What about 1? What about 0?
Excellent question!
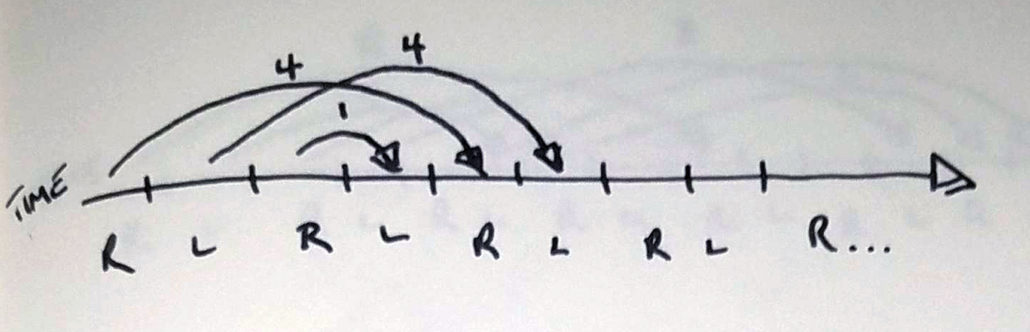
A 2 is a throw that returns to the same hand after two beats. Knowing that we’re always alternating hands, if a 2 starts in the right hand, it’ll return to the right hand before that hand can do anything else. Due to this, a 2 is an object that stays in the same hand – it’s a handhold. (…at least, that’s what we’re going to say for now. You can actually do a lot with a 2! …but let’s not get ahead of ourselves.)
A 1 is a throw that is caught exactly one beat after it’s thrown – it’s only in the air for a very small period of time. It’s odd, so it crosses… what’s the fastest way to get a ball from one hand to the other? Simply handing it across – transferring the object as though you were clapping your hands together.
A 0 is an object that returns to the same hand 0 beats later… sounds impossible, right? That’s because it is! A 0 is the absence of an object – it’s a placeholder that means that nothing happens in that hand in that beat, since there is no object present.
So far, we’ve just talked about the base patterns – “…333…” with three balls, “…444…” with four, and so on. When you go to a symphony, things get interesting when there’s more than one note that’s being played. In the same way, juggling gets a lot more interesting when you use more than just one throw.
The very first pattern that was invented (or discovered!) using siteswap notation was a three ball pattern called 441. Let’s break that down.
Remember the example at the beginning of this chapter, where we talked about jugglers ages ago using descriptions like “throw a ball kinda high on one side to the same hand, then one with the other hand at the same height to the same hand, then pass one underneath those two while they’re in the air from one hand to the other”? That’s this pattern! That’s 441!
4 – Right hand – throw this ball kinda high on one side to the same hand
4 – Left hand – …then do the same thing with the other hand – straight up and down
1 – Right hand – …then pass one underneath those two while they’re in the air, from one hand to the other.
(But wait… what about that 1 again? This is still confusing!)
What does siteswap mean, again? The numbers represent the length of time that an object takes to return to a hand after it’s been thrown. A 1 crosses from hand to hand (it’s an odd-numbered throw,) returning to a hand after 1 beat. Since we always alternate left and right hands, there’s nothing that the receiving hand could do in that time. So, a 1 is literally passed from one hand to the other.
441 is an incredible pattern, as it requires that you learn a 4 using the same beats – that is, the same metronome – as your three object cascade. Assuming that the duration of your beat is always the same (and you’ve got great technique after all – let’s make that assumption!) a 4 needs to land exactly one beat later than a 3 would. In order to execute this pattern from a three object cascade and back with a perfect rhythm (that is, without any kind of stutter or shift in the beat,) the 4 needs to be perfect.
Yes, you could achieve some form of juggling success by shifting your metronome around to accommodate imperfect throws… but in doing so, you’re learning bad habits. If you want to progress to more complicated patterns or higher numbers, you need to cultivate perfect, proportional throws.
For this reason, 441 is an excellent training pattern for a four object fountain. The fountain – the base pattern for four objects – is just a 4-beat throw executed again and again. 441 teaches you how to make a 4-beat throw perfectly, measuring it against your 3 – a throw you already have ingrained in your body.
An important note about notation
When you say 441 to a juggler, you’re literally just saying a sequence of three throws. Think of it like programming a computer – three throws programmed, three corresponding actions completed, and the activity is finished… However, if you run a pattern, you’re repeating the cycle again and again. If I were to ask a juggler to “juggle 441” or “run 441,” I’m not asking them to execute those three throws and stop completely. I’m really asking them to do …441441441441441… – running the pattern back to back for a period of time.
This might be a little pedantic and heady (okay, it’s definitely pretty pedantic and heady,) but jugglers use siteswaps both as a kind of programming language (441 = three throws and stop – one cycle of the pattern) as well as a nomenclature – a way to describe the trick as a whole (441 = running the pattern forever, the general idea of 441.)
When we refer to 441, it could really mean just one cycle of the pattern (three throws and stopping) or running it ad infinitum. This will be important information later on, especially when we talk about synchronous siteswaps and the way they’re written down.
A mathematical aside
For my math-inclined friends out there, here’s an interesting tool for you. (No, really… you’ve got to put that Rubik’s cube down first, though!) Let’s say you see a siteswap that you’re unfamiliar with… how do you find out how many objects are in that pattern? To figure this out, you need to find the siteswap’s period (that is, the number of throws the pattern has) and the sum of the beats of the pattern (that is, all the beat-values of the throws added together.)
Let’s use 441 as an example.
441 is period 3 – there are three throws in the pattern.
4+4+1 = 9
Take the sum and divide it by the period to find the number of objects in the pattern: 9/3 = 3
So, using this formula, we know that 441 is a valid siteswap for three objects.
How about something more complicated?
8448641
Period: 7
Sum: 8+4+4+8+6+4+1 = 35
Formula: 35/7 = 5
8448641 is a valid siteswap for five objects. (That means it works!)
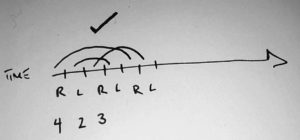
Try out these ones on your own. Are they valid? How many objects are they for?
423
634
75751
88423
97441
8641
But Thom… is this always the case?
You caught me! This is a rule of thumb. Averaging the throws is a necessary but not a sufficient condition to knowing that a pattern is valid.
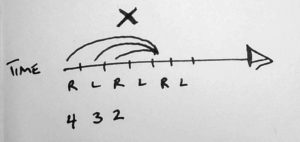
For example, 423 is a valid pattern, but 432 is not. Why is that?
In 423, there are no collisions – each ball lands in a new hand.
In 432, all of the balls end up in the same hand at the same time! It’s a mess of collisions.
If a throw with the value of n is immediately followed by n-1, for example, you’ll have a collision. Same with n followed two beats later by n-2, and so on.
Synchronous time
“So, Thom,” you say, “that’s all well and good. But I like to throw with both hands at the same time!”
An excellent point, friend. The above information pertains to juggling asynchronously – that is, one hand throwing and catching at a time. Siteswap doesn’t end there, though! Let’s dig in. (C’mon. I saw you pick that Rubik’s cube back up!)
When we juggle with a right-hand and left-hand throw at the same time, we’re putting two throws into the same beat. In order to note this, we use parenthesis and commas. Let’s use the four-ball synchronous fountain as an example.
This pattern is called (4,4). When we use synchronous notation, we still mark everything as though it were alternating hands. The hands still alternate as we write them, we’re just lumping them together into the same beat: (Right, Left)
Here’s another example – (6,4)
In this pattern, nothing crosses. The right hand only juggles 6s and the left hand only juggles 4s. How do we know how many objects this pattern is for? The brackets are confusing, but don’t let that fool you – the method we used for the asynchronous patterns works here, too:
6+4 = 10
10/2 = 5
This is a valid pattern for five balls.
In (6,4), the right hand juggles three balls (thrown at height 6) and the left hand juggles two balls (thrown at height 4.) Simple as that!
But what if we want to get the balls to cross? Let’s look at a classic, more complicated five-object pattern:
(6x,4)(4,6x)
…what does that x mean?
Since we’re lumping two throws into a single beat, we can’t have odd-numbered throws in a pattern. There’s an excruciatingly nuanced explanation for this. To sum it up, when you have an odd numbered throw in a synchronous pattern, there’s nowhere for the object to land (from the perspective of notation, at least,) since we’re bundling beats together. In order to mark the idea of a crossing throw, we stick an x behind it. If we didn’t, or so I’m told, the space time continuum would cease to exist. (…and if that happens, it’s all your fault!)
(6x,4)(4,6x) is the same series of throws, done from one side to the other – it’s a symmetrical pattern, where the throws in each beat are the same, but the hands switch what they’re doing. We can simplify the notation, indicating that the throws in the pattern are the same, just switching sides with each beat, by adding an asterisk at the end of the notation when we write it down. That gives us: (6x,4)*
A note about terminology here (and thanks to Jeff Lutkus for reminding me about this!) – If you go to a juggling convention and someone asks you about (6x,4)(4,6x), odds are they’ll just say six ex four and leave it at that. You’ll stand there and scratch your head for a moment – the pattern (6x,4) is invalid, after all! – when we talk about a pattern that’s symmetrical, flipped using an asterisk, jugglers will usually take the easy route and just say the first period of the siteswap.
…and it should be noted that this is just about the only time you’ll find a juggler taking the easy route.
Multiplexes
Okay, we’re getting really, really in deep here. (C’mon. Put that Rubik’s cube down. You’re gonna need two hands!)
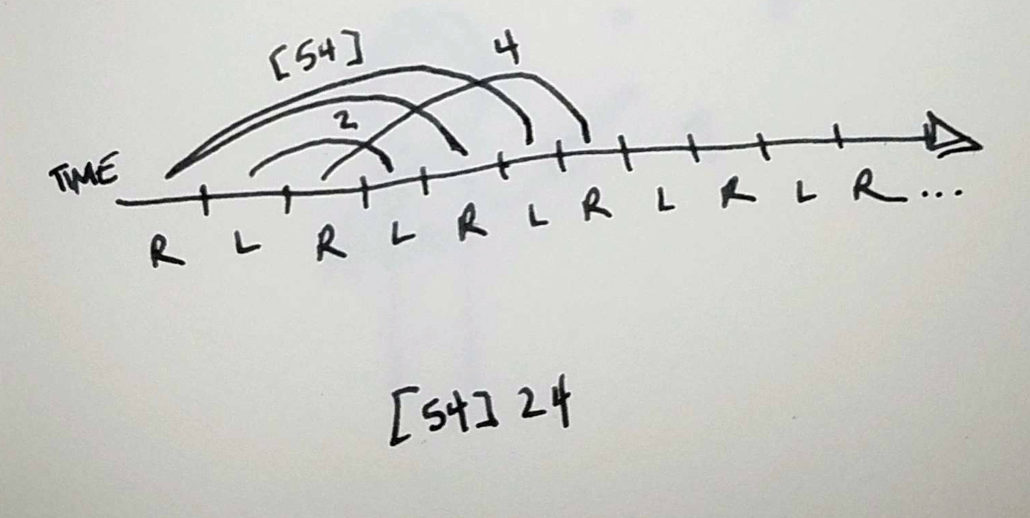
A multiplex is when you throw more than one object from a hand in a single beat. These throws are marked with brackets.
A famous five ball pattern is called the Gattoplex – named after the famous American juggler, Anthony Gatto.
[54]24
Here, the [54] means that two objects are thrown from one hand at a time. The first to leave the hand is a tall crossing 5, and the other is a 4 which goes slightly lower and returns to the same hand. If you were telling this pattern to another juggler out loud, you’d call it fifty-four, two, four. (When you say the name of a multiplex out loud, we smash the two throws into one longer number.) This seems really pedantic (and it is,) but it’s helpful when you’re talking siteswap to other jugglers. This is your life now.
FAQs and resources
What’s the notation for throws that are higher than a 9?
Excellent question! The number after 9 is 10. 10 looks like it could be two throws (1 and 0) or the multiplex [10]. To avoid confusion, we switch to letters after the siteswap 9.
10 is a, 11 is b, 12 is c, and so on.
So, the seven ball version of the classic three ball siteswap 531 is db97531. Neat, right?
Does this specific notation work if you only have one hand?
Yes, but…
There are other versions of siteswap that work for different numbers of hands more elegantly than “vanilla” siteswap does. Passers use a four-handed notation, as well as something called Prechac Notation. Other multi-handed patterns are possible – as well as a patterns using just one hand. Though you could write an incredible one-handed routine with this notation, you’d need to make some notes to the person you’re sharing it with so that they’d be able to decode it.
In one-handed siteswap, for example, a 1 is a hold and a 2 is a throw… the notation doesn’t change, but the throws look different than a two-handed pattern – no crossing, no hand-switching. The numbers still represent the amount of time an object takes to return to a hand, and that looks a bit different when there’s only one hand for the object to return to.
…That’s is all outside of the purview of this article, however, which only covers vanilla siteswap – which generally comes with the assumption that you’re using two hands.
All this writing is good and all, but is there a video where I can see this material presented differently? Preferably made by an excellent Canadian juggler? A video that was sponsored by our friends at the International Jugglers’ Association?
Of course there is!
Check out Mike Moore’s wonderful introduction to vanilla and synchronous siteswaps below!
That’s a lot of information. Can it get any more complicated?
Yes.
Mathematically speaking, is it possible to throw a ball backwards in time?
Yes.
Weird. Will knowing that make me a better performer?
Probably not.
…and that’s all there is to it! Now, go out there and conquer the world with your newfound understanding of juggling notation!
A huge thank-you to Mike Moore, Megan Gendell, Chloe Walier, and Maika Isogawa for help proofing this article!